Steve Cobb, Author at Unsplit the Vote

The NPVIC and Approval Voting

Though written without regard for alternative voting methods, maybe the National Popular Vote Interstate Compact is still OK.

Though written without regard for alternative voting methods, maybe the National Popular Vote Interstate Compact is still OK.

Why we need the NPVIC

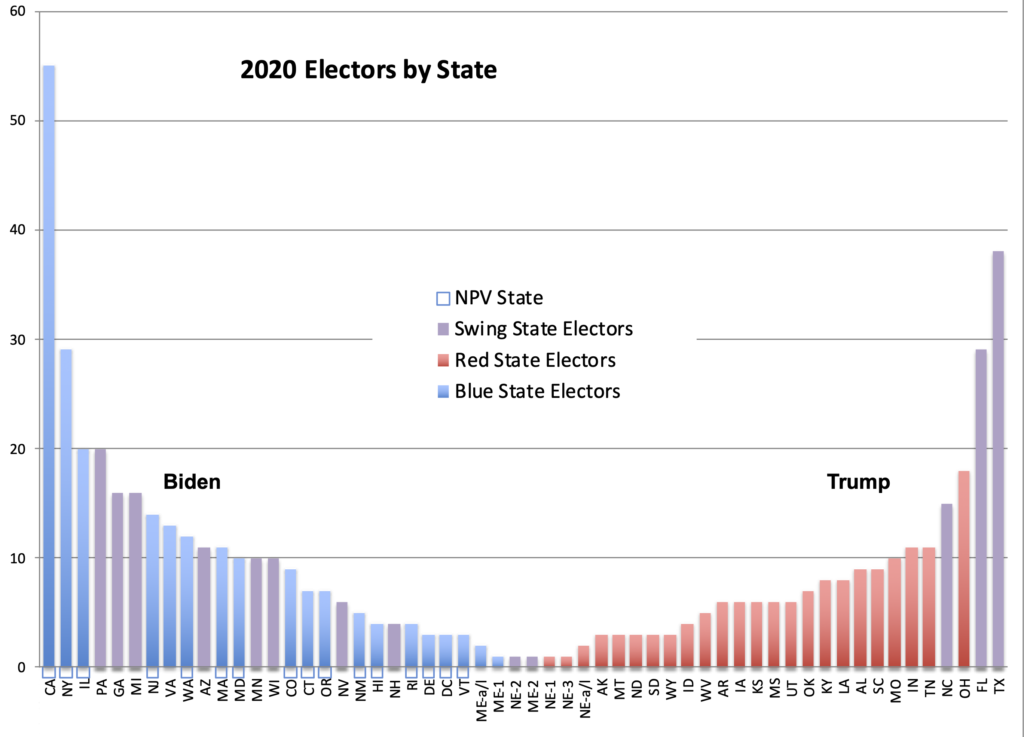
States’ winner-take-all allocation of presidential electors dates back to the early 1800s, but in our era it seems to be having an increasingly perverse effect. The Framers would have been disturbed by two consequences: excess power in 10–12 “swing states”, and voter apathy in the remaining “safe states”. The swing states attract not only additional campaign attention, but political pork and other influence. In the safe states, voters consider their votes devalued because they are unlikely to make a difference, so they are less likely to turn out. This affects the down-ballot elections. The Framers were familiar with a third problem in the Electoral College itself: its voting method, choose-one Plurality Voting (COPV), is highly vulnerable to vote splitting, and thus can fail in elections with more than two candidates. As specified in the Twelfth Amendment, the Electoral College votes only once—in the absence of a majority, the decision moves to the House of Representatives.

The National Popular Vote Interstate Compact (NPVIC) is a way to solve all three of these problems. States joining the compact agree to allocate their electors to the candidate who wins the popular vote among the NPVIC member states. Every vote would matter, even if a voter were a party’s only supporter in a state. By reducing the Electoral College to a formality, the NPVIC would mitigate its flawed voting method.

These problems may have other solutions, possibly simpler. For example:

1. A simpler interstate compact to allocate electors based on district results, like Maine and Nebraska already do, or simply proportionally. While the former approach would not completely eliminate the swing-safe problem, pushing it down to the district level might diffuse it, and it would not require cross-state vote tallying.

2. An alternative voting method, less vulnerable to vote splitting, would enable additional parties, offer voters more choices, and reduce their apathy, probably far more than would modestly increased influence in the quadrennial presidential election.

3. An alternative voting method in the Electoral College would enable it to handle multi-party elections with less concern for vote splitting. An example of this is a papal conclave of the College of Cardinals, which votes with a majority requirement and an unlimited number of rounds. However, this would require a Constitutional amendment, on top of the Twelfth.

But the NPVIC train has already left the station. As of the end of 2020, 15 states plus DC have jumped on, with 196 of the 270 electors needed for the compact to be activated. The NPVIC was launched in the wake of the 2000 election by disgruntled Democrats, but Republicans increasingly see its potential for reducing political pork. What should be done now?

The NPVIC’s flaw

The NPVIC was unfortunately written assuming the current COPV method, with no regard for alternative voting methods. The compact text says that the chief election official of each member state shall:

“determine the number of votes for each presidential slate”
“add such votes together to produce a ‘national popular vote total’ for each presidential slate”
“designate the presidential slate with the largest national popular vote total as the ‘national popular vote winner'”

Not all voting methods produce “a number of votes”. In fact, most do not. Neither the rating nor ranking methods work that way. The various methods produce various numbers, but they are apples and oranges. Tossing them all in a blender might produce an interesting smoothie, but not a useful count. But perhaps there is a way to combine different voting methods’ tallies or ballots that is not only meaningful, but unobjectionable?

Any new counting rules for combining tallies from different voting methods should be:

simple: minimal and understandable
accurate: not reduce the accuracy of the election results from those of the incumbent method
fair: not disadvantage any voter group

Two common tally formats and rulesets

Counting rules would transform the tallies or ballots from disparate voting methods into a common tally format. Obvious candidates for this format would be the minimal version of Score Voting (SV) known as Approval Voting (AV), or something resembling the incumbent voting method, COPV. The first is an evaluative (rating) method, the second an allocative (sometimes called cumulative) method. Both AV and COPV ballots assign candidates 0 or 1, but under AV the candidates are rated independently, while under COPV a ballot is a discrete token that can belong to only one candidate. Under COPV there is a fixed ‘amount’ of vote to be allocated: each of the V voters has only one ballot to allocate to one candidate.

1. An AV-based common tally format would scale the maximum tally per candidate to V. The total would be less than V*C, where C is the number of candidates, but would probably be greater than V.

2. A COPV-based common tally format would limit the total amount of vote to V. The total might be less, if some candidates’ votes got “lost” (e.g., they failed to reach some minimum threshold).

AV is probably the way to go, given COPV’s infamous vote-splitting problems. This is indeed proposed in Dr. Warren Smith’s article about NPVIC problems and solutions.

Smith suggests counting rules to combine tallies from five different voting methods, and the common tally format is a rating scaled to AV’s parameters. Combining COPV and AV tallies is simple: just add them. SV tallies must first be scaled, a simple matter. The ranked methods (Instant Runoff Voting and Condorcet methods) require substantially more calculations, but can be massaged into providing summable numbers for multiple candidates.

How about a COPV-based format, which should limit the total number of votes to V? To convert SV or AV, maybe one could scale the results by 1/(C*R), where C is the number of candidates and R is the rating scale. Converting the ranked methods here is much easier: take Smith’s rule for the top two candidates (Winner and Second), and ignore the rest.

Assessing the two counting rulesets against the three criteria

How would these counting rulesets satisfy the three criteria of simplicity, accuracy, and fairness? They are generally simple, at least no more complex than the ranked methods are already. I cannot provide a mathematical treatment, but it seems obvious that both would be more accurate than the incumbent COPV alone. Clearly Smith’s AV-based ruleset is the more accurate of the two. It “counts all the votes”.

But how about fairness? Under option two, ranked methods’ tallies would be truncated to just the top two winners, leaving weak third parties ignored and irrelevant, but making strong third parties a winner-take-all threat for second place. This might encourage a state’s strongest party to surreptitiously support a third party, as the Republicans promoted Ralph Nader in 2000. These two vote-splitting weaknesses would negate two of voting reformers’ goals: increasing choice in candidates, and reducing the swing-state effect.

Another fairness issue is the influence of one state’s system on voter behavior in another state. In all voting methods, voter choices are influenced by an expectation of what other voters will do. This is particularly true of COPV, because it is so vulnerable to vote splitting (e.g., spoilers and the wasted-vote dilemma). COPV compels voters to choose from the Schelling set—the “electable” candidates on whom like-minded voters would coordinate in the absence of communication. COPV or a ranked method with a truncating counting rule (e.g., just the top two candidates) in one state might cause voters in other states with poor voting methods to abandon favored but weak candidates, or fear of wasting their vote.

On the other hand, the existence of better voting methods in other states may expand the Schelling set, making the choice less obvious for voters in a COPV state. Would they be harmed, e.g., tempted into splitting their votes? Perhaps—despite voters having polling data showing a race to be close, vote splitting already happens occasionally in US presidential elections, most infamously in 2000. But the solution here is better voting methods, not rejecting the NPVIC.

Conclusion

I can endorse the NPVIC with Smith’s proposed counting ruleset, assuming that others find it as obvious and unobjectionable as I do. The Electoral College is fundamentally incompatible with multi-party democracy. Even if states allocated their electors proportionally to candidates’ state-level election results, and even if the Electoral College used a decent voting method, each elector would still represent only one candidate. Even if we voters used the best possible voting method, in a multi-party system the Electoral College step would muck things up. Without a Constitutional fix, the only solution is an interstate compact to decide the winner before the Electoral College, and then assign all electors to that winner. Today we are far from having a multi-party system, but to prevent more vote splitting like in 2000 we need the NPVIC.

However, we should not let the NPVIC tail wag the voting-reform dog. The presidency and vice-presidency are merely one (important) pair out of some 500K elected offices. What we need even more than the NPVIC is a sensible voting method, one much less vulnerable to vote splitting. Fortunately, it seems that the NPVIC is probably compatible with at least some alternative voting methods, most obviously Approval Voting.

A version of this article originally appeared at Democracy Chronicles.

Concurrence—a card-based coopetitive voting game

Concurrence is a card-based coopetitive voting game. Suits represent issues, and ranks represent positions on those issues.

Background

Suits are campaign issues.
Ranks are linear positions on issues.
A hand of cards is a position or preference in issue-space.
Ranks are additive, so the position of a hand with two cards of the same suit is the sum of their ranks.
The absence of a suit (void) is treated as 0 for a candidate, and null (don’t care) for a player.
The difference between two hands is their Manhattan distance in issue space.

Goal: Elect a candidate hand that minimizes your score (difference between your hand and that of the winning candidate).

Setup

For P players, T teams, and C candidates, N(P+TC) cards are needed, so use additional decks as necessary, possibly one per team.
Basic version: C=3, N=2
Divide players into roughly equal-size teams. There should be 2–8 players per team, and 2–8 teams.

Materials

Decks of cards (for simplicity, remove the face cards)
Ballots (e.g. laminated paper with dry-erase markers)
Score sheets and pens

Play

Each team agrees (unanimously) on a voting method (including a tie-breaking method), and prepares its ballots. A mature team will likely choose a default voting method, and change it rarely.

When every team is ready:

Deal Np cards face down to each player, and Nc cards face up for each of the C candidates.
Players vote silently.
Votes are tabulated, and a winning candidate is determined.

Scoring

Individual scores are the absolute difference between player hand and that of the winning candidate, on the issues (suits) that the player cares about.
Team scores are the average of the individual scores.
Option 1: Individual and team scores are tracked separately. The winner is the lowest-scoring player in the lowest-scoring team.
Option 2: Each individual receives a total score of their individual score plus the team score. The winner is the lowest-scoring player.

Repeat the play procedure for a predetermined number of rounds (say 20). Alternatively, until someone reaches a predetermined number of points (say 200).

Variations

Time limit (say 60 seconds) for voting and/or tabulation; if the players do not finish voting or tabulating in time, the winner is selected randomly, or the team is penalized points (say 10).
Candidates shared across teams or unique to each team. Shared candidates reduces the influence of chance.
Allow teams to decide separately their number of candidates C.
Reduce or increase the number of cards dealt to players (Np) and candidates (Nc).
Include face cards, worth 10 or 11–13.
Calculate score not as absolute distance but as candidate fulfilling voter preferences, with overfulfillment being better. Points are thus good, and highest score wins.
Limited polling (e.g. players reveal one or two cards).
Candidates may alter their positions (maybe automatically according to some rule, or perhaps players take turns playing the role of candidate), say by discarding one card, maybe in response to polling. Maybe player-candidates receive points for losing, zero points or even minus points for winning.
After every X rounds, players change teams in a predetermined rotation pattern.
Recount sometimes, and penalize team for errors.

Three Eras of Voting Methods

There are three kinds of voting methods—allocative, comparative, and evaluative—based on the expression form and constraint. Allocative methods give each voter a fixed amount of “vote” (continuously divisible or as discrete tokens) to allocate among candidates. Comparative methods allow voters only to show preference between pairs of candidates; generally, this is done by ranking them. Evaluative methods have voters rate candidates independently on a scale (numeric or graded). There are also hybrids, e.g. multi-stage voting methods that combine voting methods of different categories.

A voting method is a set of rules that perform three sequential functions:

Balloting: enable individual voters to express their opinions in a uniform manner
Tallying: combine the opinions into a single list
Decision: based on decision thresholds or other consensus rules, produce a result

A voting method is just one (key) piece of a voting system: the complete, interconnected set of roles, tools, and processes that gather a group’s individual opinions and preferences and distill them into a single group decision. Voting methods can be implemented physically in many different ways. While voting methods are logical rules, they may lend themselves to various physical implementations that differ in criteria like simplicity or security.

There are three kinds of voting methods— allocative, comparative, and evaluative—based on the expression form and constraint. Allocative methods give each voter a fixed amount of “vote” (continuously divisible or as discrete tokens) to allocate among candidates. Comparative methods allow voters only to show preference between pairs of candidates; generally, this is done by ranking them. Evaluative methods have voters rate candidates independently on a scale (numeric or graded). There are also hybrids, e.g. multi-stage voting methods that combine voting methods of different categories.

Allocative voting methods are the oldest, going back at least 2000 years. The word “psephology” (election science) comes from the Greek word for “pebble”, “ostracize” from the Greek word for “pottery shard”, and “ballot” from the Italian word for “little ball”—all of these voting tokens could be dropped in a candidate’s urn. The phrase “to cast one’s vote for a candidate” (shortened to “to vote for”) assumes an allocative method, where the voters give their vote tokens to a candidate. You can read more about the etymology and history of voting from Oxford. Allocative methods include the common choose-one Plurality Voting, Top Two with Runoff, and Cumulative Voting, as well as the newer Asset Voting, Liquid Democracy, PLACE, and E Pluribus Hugo.

Allocative voting methods are simple, but inherently vulnerable to vote splitting. For that reason, a key trait of allocative methods is their reallocation rule, if no candidate (or not enough candidates, in multi-winner elections) has reached the threshold to win. Reallocation can be determined by the voters or the candidates, according to preferences expressed before or after initial balloting. For example, PLACE Voting has candidates declare their “heirs” before the election, while Asset Voting allows them to negotiate after the initial tallying. TTRO has a second round of voting. Choose-one Plurality Voting has no threshold (though it is also, inexplicably, called First Past the Post), and thus no reallocation rule.

Comparative voting methods became known just over 200 years ago, at the peak of the Enlightenment. Having voters rank their candidates was an obvious balloting improvement, but how to tally them was less obvious, and highly problematic. The simplest way (convert the rankings to summable points) turned out to be deeply flawed, and the better ways were still flawed, as well as complex. In 1972 Kenneth Arrow was awarded the Nobel Memorial Prize in Economic Sciences for his Impossibility Theorem showing that no comparative voting method could simultaneously satisfy several reasonable criteria. Ranked voting methods’ problems, paradoxes, and complexities have prevented them from being widely adopted.

Evaluative voting methods are the newest, arising over 20 years ago, in the wake of mass surveys, and later the Internet. People became accustomed to rating everything on Likert scales (strongly like, like, neutral, dislike, strongly dislike) or simple binary like-or-not scales. Such scales can also be used for voting, with two huge advantages: they sum easily, and they don’t split. Evaluative methods can be divided further into two categories: scored and graded. Scored methods use a numeric scale, and each candidate’s scores are summed. Graded methods use a scale with named grades, and each candidate’s grades are counted. More complex variants exist. Another name for evaluative voting methods is Range Voting, which you can read about at The Center for Range Voting.

Honeybees use an interesting evaluative voting method when choosing a new home. Scouts head out, find candidate nesting sites, return home, and “waggle dance” to show the location and quality of a candidate. The length of the dance corresponds to the bee’s assessment of the candidate’s quality. The longer the bee dances, the greater the chance that other bees will notice, go check out the site for themselves, and return home to share their opinion. Not all bees serve as scouts, and no bee checks out every candidate site—the swarm has to economize on time and energy. However, enough bees do participate, and eventually they reach a consensus, whereupon they up and move. In a fascinating case of engineering agreeing with evolution, a similar voting method was developed by voting theorist Jameson Quinn for the Webby Awards.

Thanks to the University of South Florida’s FCIT for a clipart element.